| Bend Phenomena |
|
A number of variables can be deduced from the description of the principle that influence the bend process and the resulting quality and precision.
|
|
Stress/Strain
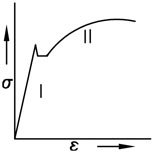
The behavior of the material during the bend process is reflected in the stress/strain curve. In this, a distinction is made between the elastic region and the plastic region. Within the elastic region, the material returns to its original state as soon as the force is lifted. The shift in the atoms in the crystal lattice is so insignificant that the atoms return to their original state when the force is lifted. In this zone, the strain increases proportionately to the stress applied in accordance with Hooke’s law: s=E.e. The slope of the line E, the elasticity modulus, is indicative of the stiffness of the material.
|
|
|
Plastic Deformation
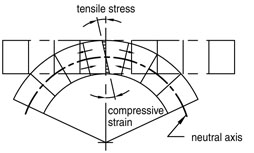 Past a certain critical value of the forces exerted, the material will show plastic deformation. This is referred to as the yield zone. Crystal lattice surfaces shift here in relation to one another to such a degree that it is impossible for the atoms to return to their original state once the force is lifted. A permanent change occurs in the crystal structure of the sheet material. When bending sheet material, under the influence of the bend force applied, strain occurs on the outer side of the bend while material is upset on the inside. In other words, there is a transition from a tensile stress to a compressive strain over the cross-section of the sheet, by which the highest values are achieved on the two surfaces. Plastic deformation therefore first occurs on the outer sides of the bend sheet, and is the greatest there during the entire bend cycle. When creating a plastic deformation, the fact must be taken into consideration that the bend force may not be so large that the tensile stress on the outside becomes so great that the ultimate stress is exceeded and cracking occurs. Naturally, thicker sheets are the most sensitive to this phenomenon. This explains why the minimum values for the bend radius to be applied for air bending and bottoming are expressed as a function of the thickness. With coining, this problem is not nearly as sensitive. there is a zone in the middle of the sheet (not exactly the geometrical middle, but close to it) with low stress. Here only elastic deformation occurs, even with high bend forces, which is why the sheet always springs back to some degree after the bend force is lifted. This will be discussed later in more detail. This springback in thin material up to approximately 2 mm / .078” can be limited to approximately 1° by selecting the right bending parameters. With thicker sheets, especially stainless steel, this will soon increase to even 3°. Corrections can be made to compensate for the springback by modifying the bend angle of the punch. Past a certain critical value of the forces exerted, the material will show plastic deformation. This is referred to as the yield zone. Crystal lattice surfaces shift here in relation to one another to such a degree that it is impossible for the atoms to return to their original state once the force is lifted. A permanent change occurs in the crystal structure of the sheet material. When bending sheet material, under the influence of the bend force applied, strain occurs on the outer side of the bend while material is upset on the inside. In other words, there is a transition from a tensile stress to a compressive strain over the cross-section of the sheet, by which the highest values are achieved on the two surfaces. Plastic deformation therefore first occurs on the outer sides of the bend sheet, and is the greatest there during the entire bend cycle. When creating a plastic deformation, the fact must be taken into consideration that the bend force may not be so large that the tensile stress on the outside becomes so great that the ultimate stress is exceeded and cracking occurs. Naturally, thicker sheets are the most sensitive to this phenomenon. This explains why the minimum values for the bend radius to be applied for air bending and bottoming are expressed as a function of the thickness. With coining, this problem is not nearly as sensitive. there is a zone in the middle of the sheet (not exactly the geometrical middle, but close to it) with low stress. Here only elastic deformation occurs, even with high bend forces, which is why the sheet always springs back to some degree after the bend force is lifted. This will be discussed later in more detail. This springback in thin material up to approximately 2 mm / .078” can be limited to approximately 1° by selecting the right bending parameters. With thicker sheets, especially stainless steel, this will soon increase to even 3°. Corrections can be made to compensate for the springback by modifying the bend angle of the punch.
|
|
Bend Force
The bending force necessary to achieve plastic deformation in a certain sheet material is dependent on the nature of the material (in particular the tensile strength), its thickness and length, the V opening width and the desired bend angle. (The tensile stress is a reflection of the forces with which the atoms in the crystal lattice are attached to one another, thus the strength of the crystal lattice; this is also known as the deformation resistance). The bend force required can be calculated based on the following formula: F = C.s2.l.Rm/V. In this formula, F is the bend force (in kN), s is the thickness (in mm), l is the length of the sheet (in m), Rm is the tensile strength of the material (in kN/cm2) and V is the width of the opening (in mm). C is a constant that, in turn, is dependent on the sheet thickness and width of the opening, based on the formula C = 1 + 4s/V. In any event, the formula for F clearly demonstrates the correlation between the bending force and the various process parameters. For air bending of sheet steel the formula renders a rule-of-thumb value for the bend force of 80 kN per meter of length to be bent and per mm of sheet thickness. In determining the bend forces necessary with a press brake, GUANG BEI’s Press Brake Productivity Slide serves as a simple and practical instrument (available with metric and inch measurements). It must also be noted that the material’s tensile strength increases as the strain increases. This is related to the fact that the crystal lattices and the sliding surfaces between them deform more and more, as a result of which deformation becomes increasingly difficult to achieve and requires more energy. This phenomenon is referred to as stiffening of the material. The extent to which this phenomenon occurs is dependent not only on the nature of the material, but also on the process parameters, including the temperature and the speed of the deformation
|
|
|